从 Uniswap v3 到 crvUSD LLAMMA

作者介绍：

[email protected] : 机制审计、产品设计、密码经济学独立研究员。

[email protected] : 代币经济学独立研究员，初级 Solidity 工程师，伦敦帝国理工学院金融科技硕士生。

[email protected] : 独立开发者，DappLearning 核心贡献者。

[email protected] : Solidity 开发者、安全研究员、DeFi 爱好者。

前言

Curve 稳定币最难的部分是 LLAMMA（AMM for continuous liquidation/deliquidation）。LLAMMA 参考了 Uniswap v3 中的一些原则。但是，白皮书中的价格与 Uniswap v3 白皮书中的算法不同。我们将统一这两个项目，并尝试了解 Curve CEO 是如何设计这个演算法。

用 Uniswap v3 作为参考

本文中价格的定义与 Uniswap v3 互为倒数。因此，我们修改了 Uniswap v3 白皮书中的公式，让它与本文保持一致。简而言之，LLAMMA 试图让 Uniswap v3 中的一切都变得动态，以便为 crvUSD 债务人和清算人提供更适当的价格。

恒定乘积公式 (Constant Product Fomula) 比较

Uniswap v3 白皮书中的公式 (2.2)：

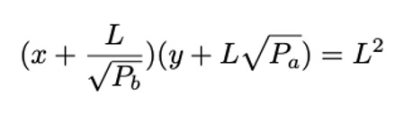
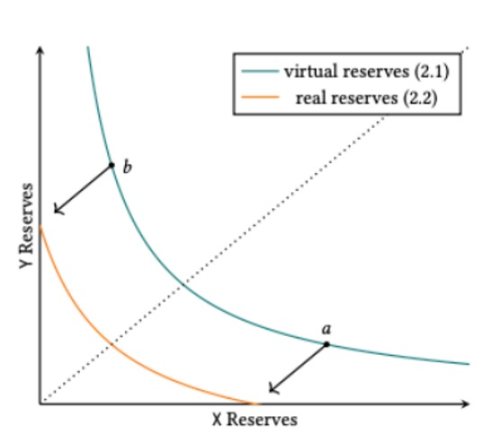
图一：Uniswap v3 虚拟流动模拟

Curve 稳定币白皮书中的公式 (1)：

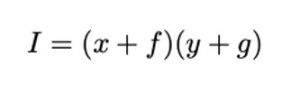
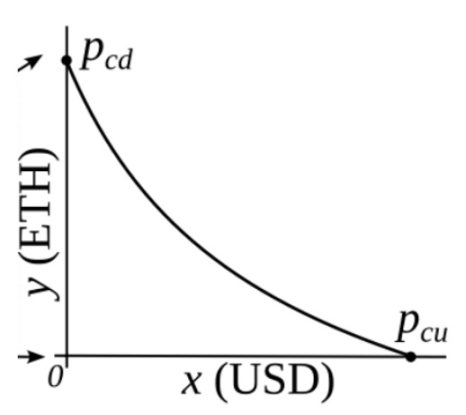
图二: 有外部价格来源的 AMM

在这裡 Pcd 代表 Pcurrent_down, Pcu 代表 Pcurrent_up

而对应关係为：

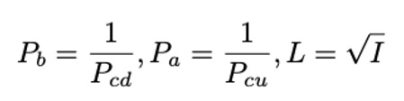
对应的恒定乘积公式为：

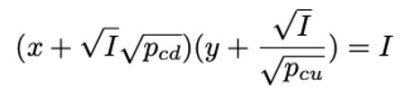
而在这之间：

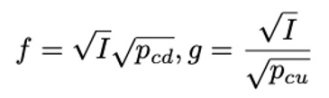
流动性计算公式对应

Uniswap v3 白皮书中的公式 (6.7) ：

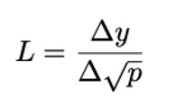
由于它们的价格定义之间存在倒数关係，对应的公式为：

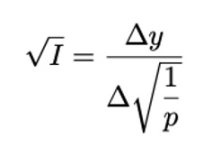
此公式的一个具体应用是：

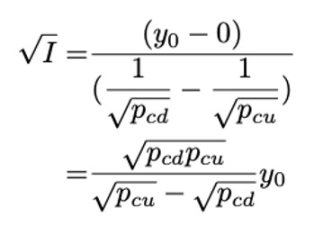
平方展开可以得到：

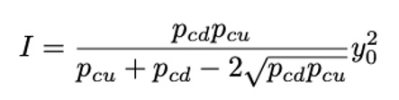
从上面的公式我们很容易的可以了解，当 y0 保持不变，Pcd 和 Pcu 数值越接近，相对应的流动性 I 则越大。

换句话说：

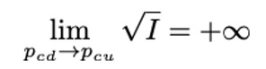
流动性不可能是无限的,在 Uniswap V3 中对应最小的 tick 会限制 L 的大小。

由此可以推断在 LLAMMA 中，我们还需要定义一个指标来衡量价格之间的最小差异，来继续 Uniswap v3 和 Curve 的类推。

对应最小差价

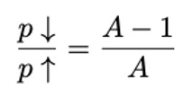
从 A 的定义中可以看出, 当 p↓ 和 p↑ 越接近时 ， A 则越大，流动性集中度越高：

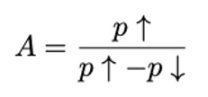
Uniswap v3 中，只有能被 tickSpacing 整除的 tick 才能被预设。因此，tickSpacing 决定了 LP 分配流动性的最低价格范围。tickSpacing 越小，价格范围越窄、越精确。在 Uniswap v3 中，不同的费用等级决定了不同的 tickSpacing。

然而，crvUSD LLAMMA 不需要那麽多 tickSpacing。由于 LLAMMA 仅有 ETH-crvUSD, 因此只需要让每一个 tickSpacing = 100basepoint。

来自 Uniswap v3 的公式 (6.1)：

关于【从 Uniswap v3 到 crvUSD LLAMMA】的延伸阅读

• Base 链 DEX —— Aerodrome VS Curve

  Velodrome是一个成功的DeFi案例，通过改进veCRV模板，实现了更优越的DEX模式。与Curve不同，Velodrome的流动性提供者不收取交易费用，而是通过VELO代币排放获得激励。通过仪表投票，veCRV/veVELO持有者决定每周发行的CRV/VELO代币分配比例。Velodrome避免了其他协议吞噬供应的可能性，并提供了类似于Convex的功能，但更简单。它正在成为超级链的基础流动性中心，可能会改变游戏规则。Velodrome已在Optimism上取得巨大成功，其产品套件包括收取和分配费用的DEX部分。

• 流动性提供者的博弈，Curve债务难题何解？

  当场外交易的CRV变得可流动时，Curve将不得不经历另一次压力测试。

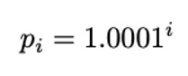
在 LLAMMA 中，A=100，来自 Curve 稳定币白皮书的公式 (11)：

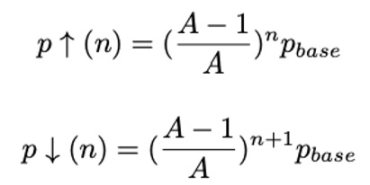
设置 n = -i, A=100, 我们会得到：

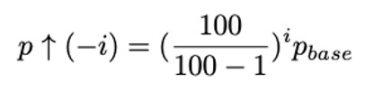
设计 Pcd 和 Pcu

我们希望 LLAMMA 具有以下属性：当 ETH 价格上涨时，矿池购买 ETH。当 ETH 下跌时，矿池出售 ETH。在这样的机制下，我们把 Pcd 和 Pcu 定义为 Po 的函数并且比线性函数更陡峭，因此它们的增长率会比 Po 更快。 同时从图中可以看出两条曲线 Pcu 和 Pcd 分别通过两点 ( P↓ , P↓ ) 和 ( P↑ , P↑ ) 。满足以上要求的 Pcd 和 Pcu 其实有很多曲线。通用公式为：

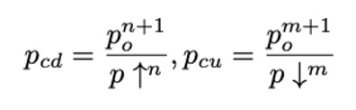
当 m < n

让我们从最简单的例子开始：

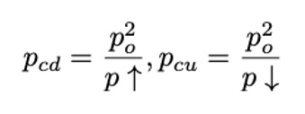
把 Pcu 和 Pcd 带入 I 的平方展开：

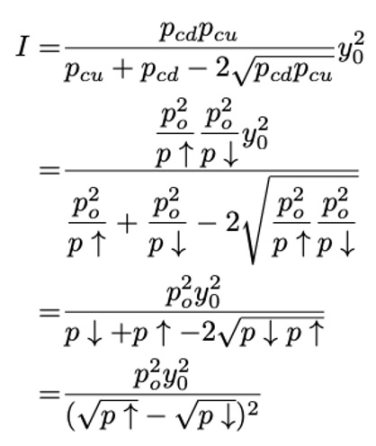
然后 f² 可以计算为：

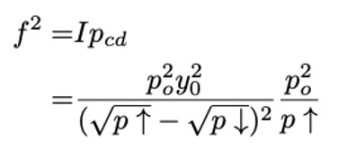
不难发现 f² 在这种假设下很难理解和计算。如果 Pcu 和 Pcd 是Po 的三次函数:

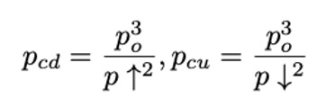
把 Pcu 和 Pcd 带入 I 的平方展开：

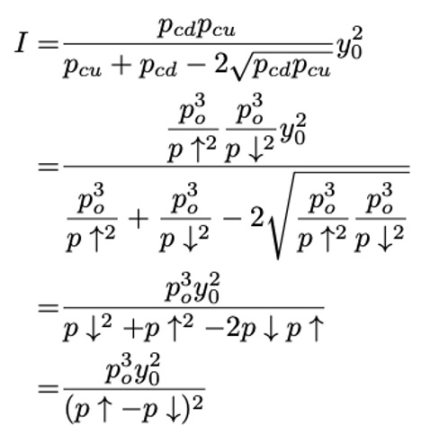
重新计算 f²：

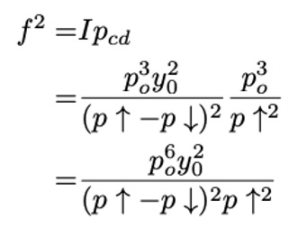
可以看出，当Pcu 和 Pcd 是 Po 的三次函数，整个数学形式就简单多了。去掉了平方根项，计算方便多了。如果接受更高的订单，则 AMM 的价格和 Po 将相差很大，因此购买 ETH 的成本（当价格上涨时）会更高，而导致更大的清算损失。总之，把 Pcu 和 Pcd 定义为 Po 的三次函数是一个更好的选择。

其他参数的推导

Pcu 和 Pcd 是关于 Po 的三次函数, 取特别数值 Po = P↑, 不难得到 Y = Y0 和 X = 0，于是：

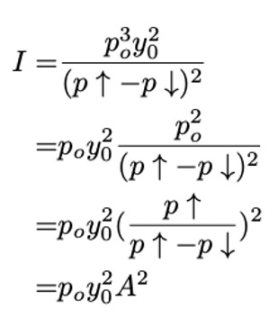
鉴于 I 的公式，我们可以计算 f 和 g：

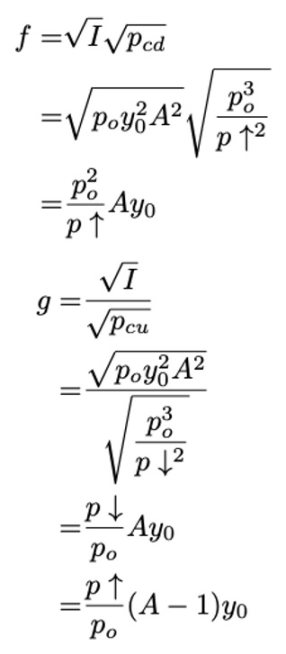
在这边，我们最终得到完整的恒定乘积公式：

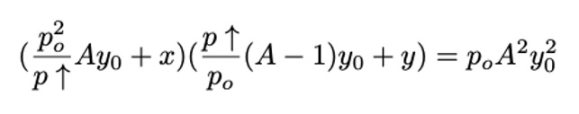
将上方公式转化为 Y0 二次方程式：

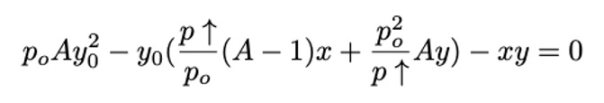
用一个未知数的二次方程求解 Y0：

如果价格变动的够慢让预言机价格 Po 完全有能力遵循它，给定 X 和 Y，使用 Uniswap v3 的计算公式，是有可能计算出 ETH 的 Y↑ 是多少（如果价格上涨）或美元的 X↓ 最终将处于的区间内（如果价格下跌）：

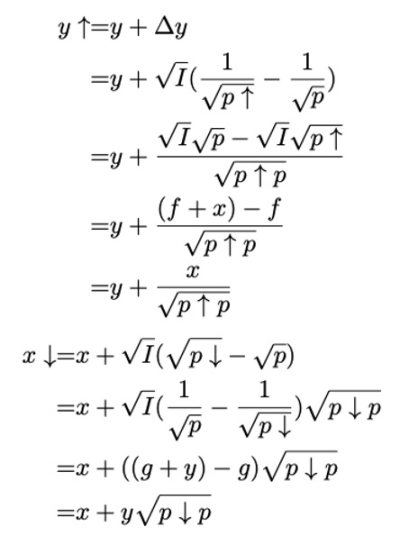
参考出处：

Adams, Hayden, et al. "Uniswap v3 core." Tech. rep., Uniswap, Tech. Rep, 2021 from https://uniswap.org/whitepaper-v3.pdf

Egorov, Michael, and Curve Finance. Curve stablecoin design. Technical report, Curve Finance, Tech. Rep, 2022 from

https://github.com/curvefi/curve-stablecoin/blob/master/doc/curve-stablecoin.pdf

免责声明：本文仅代表作者个人观点，不代表链观CHAINLOOK立场，不承担法律责任。文章及观点也不构成投资意见。请用户理性看待市场风险，以及遵守所在国家和地区的相关法律法规。
图文来源：0xmc等，如有侵权请联系删除。转载或引用请注明文章出处！

标签：CurveUniswap精选